Here’s How Two New Orleans Teenagers Found a New Proof of the Pythagorean Theorem

April 12, 2023

Here’s How Two New Orleans Teenagers Found a New Proof of the Pythagorean Theorem

An inspirational example of how elementary math is open to everyone

Recently, two teenage girls — Calcea Johnson and Ne’Kiya Jackson — gave a presentation to the American Mathematical Society where they demonstrated a new proof of the Pythagorean Theorem. Their proof has caused quite a stir.

One reason for the stir delights me and makes me incredibly happy as a teacher of mathematics. By all accounts, these two teenage math students are the exact opposite of the majority of the math establishment. They are female, they are African-American, and they come from an area which is not particularly renowned for producing high academic achievers. This is just an awesome turn of events and one which should inspire anyone — no matter what their gender, ethnic or socio-demographic background — that excellence in your chosen field of study is always attainable if you have enough joy and passion for what you do.

Another reason for the stir is that the proof these young trailblazers have proposed might make a few established mathematicians eat their words.

This is because their proof uses trigonometry.

Now why is that such a big deal? Well, many of our trigonometric identities and laws depend on the Pythagorean Theorem, and so a number of mathematicians have suggested that any proof of the theorem using trigonometry is circular logic. Put another way, they argue that using trigonometry to prove Pythagoras is basically using A to prove B, when A already depends on B. One strong proponent of this point of view was the mathematician Elisha Loomis, who published a book in 1927 full of non-trigonometric proofs of the theorem, and explicitly stating that trigonometric proofs were impossible.

However, this point of view has been increasingly questioned in recent decades, and a few trigonometric proofs of Pythagoras have made the rounds since then. Claims in the media that Johnson and Jackson’s proof is the first trigonometric proof of Pythagoras are overblown, but their proof could well be the most beautiful and simplest trigonometric proof we have seen to date, and is clearly the work of young, sharp minds uncomplicated by the years of deep research that characterise the work of many experienced mathematicians.

In this article, I’ll do a quick reminder of what the Pythagorean Theorem is, before doing my best to explain how Johnson and Jackson proved it using simple trigonometry. Although their proof hasn’t been published (I hope it will be!), I’ve pieced together their approach from various online discussions of their talk.

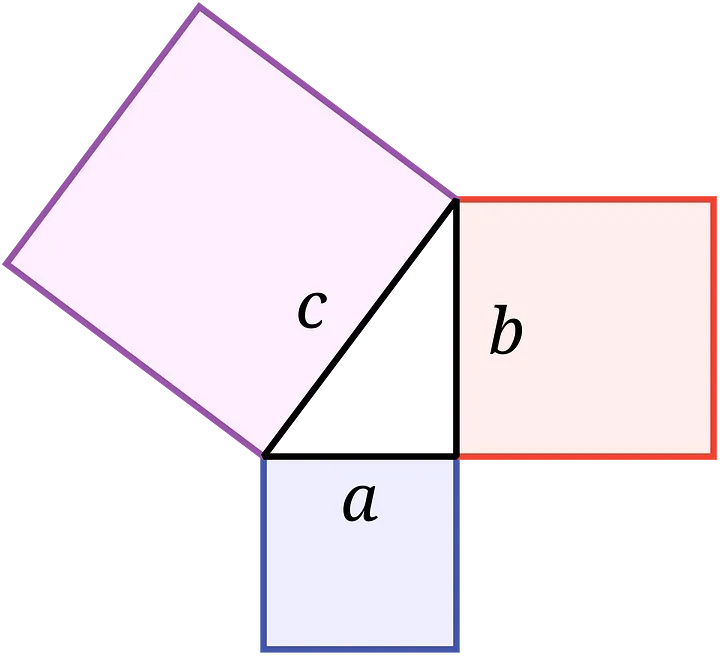
Pythagorean Theorem: In a right angled triangle, the square of the longest side is equal to the sum of the squares of the other two sides

What is the Pythagorean Theorem?

The Pythagoerean Theorem is over 2500 years old and relates the sides of a right angled triangle. It states that the square of the longest side (the hypotenuse, or c in the above diagram) is equal to the sum of the squares of the other two sides. So a² + b² = c².

This is routinely taught at schools from very young ages, along with simple integer examples of the theorem, such as 3² + 4² = 5² and 5²+ 12²= 13². These integer solutions are often known as Pythagorean Triples.

Referring to the triangle above, let ⍺ be the angle between the side of length a and the side of length c. Then if we use our trigonometric ratios, we have sin⍺ = b/c and cos⍺ = a/c. So sin²⍺ + cos²⍺ = (a² + b²)/c² = 1. Therefore the popular identity sin²⍺ + cos²⍺ = 1 is derived from the Pythagorean Theorem and any proof of the Pythagorean Theorem that uses this identity or any identity derived from it is indeed invalid due to circular logic. That said, the sine and cosine ratios themselves can be shown to be independent of the Pythagorean Theorem, and so there is no reason why we cannot use these ratios in a proof, as long as it doesn’t make reference to Pythogorean-derived trig identities.

What is this new proof?

OK, so here’s how I think it goes. Have a look at this diagram and refer to it all the way through this proof:

Let’s start with our simple right-angled triangle in the top left with sides a,b and c (hypotenuse), as pictured. Let’s assume for now that a ≠ b — we will deal with the trivial special case of a = b in a note at the end of this article. Let the angle between the sides of lengths b and c be ⍺, and let the angle between the sides of lengths a and c be β, also as pictured. Now we make three geometric steps from this original right-angled triangle:

We reflect in the side of length b, to form the top right equivalent triangle.

We extend a line perpendicular to the side of length c in the original triangle.

We extend a continuous line from the hypotenuse of the reflected triangle.

When our extended lines from steps 2 and 3 meet, we form a new larger right angled triangle of hypotenuse length C and sides A and c as pictured.

Within this larger right angled triangle, we draw a series of smaller and smaller, similar right angled triangles as pictured, forming an infinite sequence of similar triangles of decreasing size.

We are now going to investigate how to derive the lengths A and C using this infinite sequence of similar triangles.

Deriving lengths of the sides of the smaller triangles

If we look at the first right-angled triangle from the top left of side length A, this triangle has a side of length 2a, and therefore its hypotenuse is of length 2a/sinβ. But from our original triangle we know that sinβ = b/c, so we can conclude that this hypotenuse is length (2ac)/b. This leads to the third side of this triangle to be 2a²/b.

If we move immediately to the triangle on the right, we know that one of the shorter sides is length 2a²/b and therefore the hypotenuse of this triangle (a segment of side length C), is 2a²/(bsinβ) = (2a²c)/b².

This process can be continued, but it becomes apparent that each of the smaller similar triangles decrease by a factor of a²/b². This means that length A is a geometric series with first term (2ac)/b and common ratio a²/b². Similarly, length C starts with c and is then a geometric series with first term (2a²c)/b² and common ratio a²/b².

Calculating lengths A and C

Now we can use our formulas for the sums of geometric series to calculate lengths A and C. The formula for the sum of geometric series of initial term k and common ratio r is k/(1-r). This sum converges when r has absolute value less than 1, and since r is in this case a²/b², we can always be sure it converges (if a>b then just swap them).

So let’s calculate length A. In this case k = (2ac)/b and r = a²/b², so

Using a similar approach with k = (2a²c)/b² and remembering that we need to add c at the beginning, we get

Wrapping up this beautiful proof

Now look what happens when we take the ratio of A to C:

But we can see from our original diagram that this is sin(2⍺).

Now, let’s look at the sine rule on the top icoceles triangle formed from reflecting our original right-angled triangle. Note that the sine rule is not dependent on right angled triangles. The sine rule states that, in any triangle, the ratio between a side and the sine of its opposite angle is always the same.

Therefore:

So, transferring what we now know into this formula we have:

which simplifies to:

Noting that the neither a, b nor c are zero in this situation, and noting that the numerators are identical, leads to the conclusion that the denominators are identical. This proves the Pythagorean Theorem.

[Note: In the special case a = b, where our original triangle has two shorter sides of length a and a hypotenuse, the proof is more trivial. In this case we simply focus on the larger isoceles triangle at the top formed by reflecting the original in one of the sides of length a. Using this larger right-angled triangle, where both of the non-right angles are ⍺, we have that sin⍺ = a/c = c/2a. This gives 2a² = c² as required. My thanks to Medium user

Wotsit

for pointing out the need to deal with this special case.]

Many congratulations to Johnson and Jackson!

What did you think of Johnson and Jackson’s proof of the Pythagorean Theorem? Feel free to comment!

Cari Blog Ini

artikelbrilian.id

Here’s How Two New Orleans Teenagers Found a New Proof of the Pythagorean Theorem

Komentar

Posting Komentar

Postingan Populer

Teaching ChatGPT to Speak my Son’s Invented Language